PHYSICAL WORLD, Units and Measurements
Physics
Physics deals with the study of the basic laws of nature and their manifestation in different phenomena. The basic laws of physics are universal and are applied in widely different contexts and conditions.
Physics, Technology and Society
PHYSICAL WORLD, Units and Measurements
Science, Technology and Society have strong relationships among one on other. Science is the mother of technology and both of them are the reasons for the creation and development of the society.
Science and technology issues are actually discussed worldwide today. Progress in this has led to produce the ability to integrate different types of physical products.
Physics is a basic discipline in the category of natural sciences which also includes other disciplines like Chemistry and Biology. The word physics comes from a Greek word meaning nature.
Fundamental forces in nature :
There are four fundamental forces in nature. They are the ‘gravitational force’, the ‘electromagnetic force’, the ‘strong nuclear force’, and the ‘weak nuclear force’. Unification of different forces/domains in nature is a basic quest in physics.
Nature of physical laws :
(i) The physical quantities that remain unchanged in a process are called conserved quantities. Some of the general conservation laws in nature include the laws of conservation of mass, energy, linear momentum, angular momentum, charge, etc. Some conservation laws are true for one fundamental force but not for the other.
(ii) Conservation laws have a deep connection with symmetries of nature. Symmetries of space and time, and other types of symmetries play a central role in modern theories of fundamental forces in nature.
1.Some physicists from different countries of the world and their major contributions
Name Major Discovery Country of
Origin
Archimedes Principle of buoyancy; Principle of the lever Greece
Galileo Galilei Law of inertia Italy
Christiaan Huygens Wave theory of light Holland
Isaac Newton Universal law of gravitation ; Laws of motion ;
Reflecting telescope U.K.
Michael Faraday Laws of electromagnetic induction U.K.
James Clerk Maxwell Electromagnetic theory; Light – an electromagnetic wave U.K.
Heinrich Rudolf Hertz Generation of electromagnetic waves Germany
J.C. Bose Short radio waves India
W.K.Roentgen X-rays Germany
J.J. Thomson Electron U.K.
Marie sklodowska Curie Discovery of radium and polonium;
Studies on natural radio activity poland
Albert Einstein Explanation of photoelectric effect;Theory of relativity Germany
Victor Francis Hess Cosmic radiation Austria
R.A. Millikan Measurement of electronic charge U.S.A.
Ernest Rutherford Nuclear model of atom New Zealand
Niels Bohr Quantum model of hydrogen atom Denmark
C.V. Raman Inelastic scattering of light by molecules India
Louis Victor de Broglie Wave nature of matter France
M.N. Saha Thermal ionisation India
S.N. Bose Quantum statistics India
Wolfgang Pauli Exclusion principle Austria
Enrico Fermi Controlled nuclear fission Italy
Werner Heisenberg Quantum mechanics; Uncertainity principle Germany
Paul Dirac Relativistic theory of electron; Quantum statistics U.K.
Edwin Hubble Expanding universe U.S.A.
Ernest Orlando Lawrence Cyclotron U.S.A.
James Chadwick Neutron U.K.
Hideki Yukawa Theory of nuclear forces Japan
Homi Jehangir Bhabha Cascade process of cosmic radiation India
Lev Davidovich Landau Theory of condensed matter; Liquid helium Russia
S.Chandrasekhar Chandrasekhar limit, structure and evolution of stars India
John Bardeen Transistors ; Theory of super conductivity U.S.A.
C.H. Townes Maser; Laser U.S.A.
Abdus Salam Unification of weak and electromagnetic interactions Pakistan
Link between technology and physics
Technology Scientific principle (s)
Steam engine Laws of thermodynamics
Nuclear reactor Controlled nuclear fission
Radio and Television Generation, propagation and detection of electromagnetic waves
Computers Digital logic
Lasers Light amplification by stimulated emission of radiation
Production of ultra high Superconductivity
magnetic fields
Rocket propulsion Newton’s laws of motion
Electric generator Faraday’s laws of electromagnetic induction
Hydroelectric power Conversion of gravitational potential energy into electrical energy
Aeroplane Bernoulli’s principle in fluid dynamics
Particle accelerators Motion of charged particles in electromagnetic fields
Sonar Reflection of ultrasonic waves
Optical fibres Total internal reflection of light
Non-reflecting coatings Thin film optical interference
Electron microscope Wave nature of electrons
Photocell Photoelectric effect
Fusion test reactor (Tokamak) Magnetic confinement of plasma
Giant Metrewave Radio Detection of cosmic radio waves
Telescope ( GMRT)
Bose-Einstein condensate Trapping and cooling of atoms by laser beams and magnetic fields
Units and Measurements
Fundamental quantities
The physical quantities which are independent of other quantities are called fundamental quantities.
Example: Mass, length, time etc.
Quantities are those which can be measured using an instrument. Any physical phenomenon or observation that can be measured using an instrument is called quantity.
Derived quantities
The physical quantities which are derived from fundamental quantities are known as derived quantities.
Example: Density, volume, speed, force etc.
The SI system of units
In 1971, General conference of weights and measures introduced a logical and rationalized system of units known as international system of units, abbreviated as SI in all languages. In this system, there are seven fundamental quantities and two supplementary quantities.
Fundamental quantities and their units
S. No. |
Physical quantity |
Unit |
Symbol |
| 1. | Length | Metre | m |
| 2. | Mass | Kilogram | Kg |
| 3. | Time | Second | s |
| 4. | Temperature | Kelvin | K |
| 5. | Electric current | Ampere | A |
| 6. | Luminous intensity | Candela | Cd |
| 7. | Amount of substance | Mole | mol |
Supplementary quantities and their units
S. No. |
Physical quantity |
Unit |
Symbol |
| 1. | Plane angle | radian | rad |
| 2. | Solid angle | Steradian | Sr |
Rules of writing unit
In writing the unit of any quantity, small letters must be used for symbol of unit. Eg., m, ms–1
Symbols are not followed by full stop.
If any unit is named after a scientist, its symbol should be initial capital letter. Eg., N(newton), W(watt), K(kelvin) etc.
The full name of a unit always begins with a small letter, even if it is named after a scientist. , 5 N or 5 newton.
Symbols do not take plural form.
Some practical units
There are some practical units which are simultaneously used with SI units.
(i) 1 fermi = 10–15 m
(ii) 1 angstrom = 10–10 m
(iii) 1 nanometer (nm) = 10–9 m
(iv) 1 micron (mm) = 10–6 m
(v) 1 light year = 9.46 ´ 1015 m
(vi) 1 astronomical unit (AU) = 1.496 ´ 1011 m
(vii) 1 parsec = 3.03 ´ 1018 m
(viii) 1 amu = 1.66 ´ 10–27 kg
(ix) 1 quintal = 100 kg
(x) 1 tonne = 1000 kg
(xi) 1 lunar month = 27.3 days
(xii) 1 Shake = 10–8 s
The two supplementary SI units are defined as follows
(i) Radian (rad) : 1 radian is the angle subtended at the centre of a circle by an arc equal in length to the radius of the circle. Thus,
(ii) Steradian (Sr) : 1 steradian is the solid angle subtended at the centre of a sphere by a surface of the sphere equal in area to that of a square, having each side equal to the radius of sphere.Thus,
Dimensions of a physical quantity
The dimensions of a physical quantity are the powers to which the unit of fundamental quantities are raised to represent that quantity.
Dimensions of fundamental quantities
S. No. |
Quantity |
Dimensional formula |
| 1. | Length | [L] |
| 2. | Mass | [M] |
| 3. | Time | [T] |
| 4. | Electric current | [A] |
| 5. | Temperature | [K] |
| 6. | Luminous intensity | [Cd] |
| 7. | Amount of substance | [mol] |
| 00. | The supplementary quantities i.e., plane angle and solid angle have no dimensions. |
Dimensional equation
The equation obtained by equating a physical quantity with its dimensional formula is called dimensional equation of the given physical quantity. Example: Force = [MLT–2]
Dimensions of force are 1, 1 and –2 in mass, length and time respectively. Dimensional formula of force is [MLT–2].
“Force = [MLT–2]” is called dimensional equation.
Dimensional formulas of some physical quantities
S. No. |
Physical quantity |
Relation with other quantities |
Unit |
Dimensional formula |
| 1. | Force | Mass ´ acceleration | N | [MLT–2] |
| 2. | Work | Force ´ displacement | J | [ML2T–2] |
| 3. | Pressure | Force/area | Nm–2 | [ML–1T–2] |
| 4. | Force constant | Force/length | Nm–1 | [ML0T–2] |
| 5. | Gravitational constant, G | Nm2 kg–2 | [M–1L3T–2] | |
| 6. | Impulse | Force ´ time | Ns | [MLT–1] |
| 7. | Stress | Force/area | Nm–2 | [ML–1T–2] |
| 8. | Strain | – | [M0L0T0] | |
| 9. | Modulus of elasticity | Stress/strain | Nm–2 | [ML–1T–2] |
| 10. | Surface tension | Force/length | Nm–1 | [ML0T–2] |
| 11. | Coefficient of viscosity | Ns m–2 | [ML–1T–1] | |
| 12. | Latent heat | J kg–1 | [M0L2T–2] | |
| 13. | Electric charge | Current ´ time | C | [M0L0TA] |
| 14. | Electric potential | Work/charge | JC–1 or V | [ML2T–3A–1] |
| 15. | Resistance | Potential/current | ohm(W) | [ML2T–3A–2] |
| 16. | Capacitance | Farad (F) | [M–1L–2T4A2] | |
| 17. | Inductance, L | Henry (H) | [ML2T–2A–2] | |
| 18. | Magnetic field, B | Tesla (T) | [ML0T–2A–1] | |
| 19. | Planck’s constant, h | Js | [ML2T–1] |
Four types of physical quantities
(1) Dimensional constants:
These are the physical quantities whose values are constant but they possess dimensions. Eg., Gravitational constant (G), Stefan’s constant (s) etc.
(2) Dimensional variables:
These are the quantities whose values are variable and they possess dimensions. Eg., Volume, acceleration, force etc.
(3) Dimensionless constants:
These are the physical quantities whose values are constant but they do not possess dimensions. Eg., 1, 2, 3, …… p etc.
(4) Dimensionless variables:
These are quantities whose values are variable and they do not have dimensions. Eg., Angle, strain, relative density etc.
Principle of homogeneity of dimensions
According to this principle, the dimensions of all the terms occurring on both sides of the equations must be same.
Uses of Dimensional Analysis
(1) Conversion of unit of a derived physical quantity from one system of unit to another system of unit is based on the fact that product of numerical value contained in and the unit of physical quantity remains constant i.e., larger unit has smaller magnitude.
or
Q = n1u1 = n2u2
where n1, n2 are numeric values and u1, u2 are the two units of measurement of the physical quantity Q.
(2) To check the correctness of a physical relation. This is based on the principle of homogeneity of dimensions.
(3) Deriving the relation among the physical quantities: We can derive an expression of a physical quantity if we know the various factors on which it depends, by using the principle of homogeneity.
Let physical quantity X depends on other quantities P, Q and R, then we can write X = K Pa Qb Rc.
Where K is a dimensionless constant, whose value can be determined by experiment or otherwise, but not by dimensions. By equating dimensions of both sides of equation, we can get required relation among the quantities.
Limitations of the dimensional analysis
By the method of dimensions, we cannot get any information about the dimensionless constant.
If a physical quantity depends on more than three factors, all having dimensions, the formula cannot be derived.
We cannot derive the formulas containing trigonometric functions, exponential functions, logarithmic functions etc.
The method of dimensions can’t be used to derive the relation like . [i.e., equations containing more than one term with + or – symbol on right side].
It gives no information whether a physical quantity is a scalar or vector.
Order of magnitude
It gives an idea about how big or how small a magnitude is. A number N can be expressed as:
N = n ´ 10x
If 0.5 < n £ 5, then N will be the order of magnitude of x.
The speed of light c, gravitational constant G and Planck’s constant h are taken as the fundamental units in a system. Find the dimensional formulas of length and time in this new system of units.
Solution
c = [LT–1] … (i)
G = [M–1L3T–2] … (ii)
h = [ML2T–1] … (iii)
From equation (i), c3 = [L3 T–3]
From equations (ii) and (iii) Gh = [L5T–3]
Gh = [L5 T–3]
c5 = [L5 T–5]
Check the equation v2 = u2 + 2as is dimensionally correct or not. [Symbols have their usual meanings]
Solution
v2 = u2 + 2as
Dimensions of LHS = [LT–1]2 = [L2T–2] . . . (i)
Dimensions of RHS = [LT–1]2 + [LT–2] [L] = [L2 T–2] + [L2 T–2]
= [L2 T–2] . . . (ii)
From (i) and (ii) it is clear that the given equation is dimensionally correct.
If the centripetal force depends on the mass (m), velocity (v) and radius of path (r) for an object, find the formula for it.
Solution
Let force F = k (mass)a (velocity)b (radius)c
Writing dimensions on both the sides,
[MLT–2] = k [M]a [LT–1]b [L]c
[M1L1T–2] = k [Ma Lb+c T–b]
Comparing the powers on both the sides
a = 1, b + c = 1 and – b = – 2
b = 2 Þ 2 + c = 1 Þ c = – 1
\ a = 1, b = 2, c = – 1
\ F = k m1 v2 r–1 or k is a dimensionless constant.
The value of gravitation constant is G = 6.67 ´ 10–11 Nm2 kg–2 in SI units. Convert it into units of CGS system.
Solution
G = [M–1 L3 T–2]
Let
Let 1 corresponds to SI system and 2 to CGS system
n1 = 6.67 ´ 10–11, M1 = 1 kg, L1 = 1 m, T1 = 1 s, M2 = 1g = 10–3 kg, L2 = 1 cm = 10–2 m and T2 = 1 s
Now,
\ n2 = 6.67 ´ 10–11 [10–3] [106] [1] = 6.67 ´ 10–8
Thus, value of G in CGS system is 6.67 ´ 10–8 dyne cm2 g–2.
The velocity v of a particle depends upon the time t according to the equation Write the dimensions of a, b, c and d.
Solution
From principle of homogeneity, [a] = [v]
or [a] = [LT–1]
[bt] = [v]
or [bT] = [LT–1]
or [b] = [LT–2]
[d] = [t]
or [d] = [T]
[c] = [v] [d + t] = [LT–1] [T]
[c] = [L]
Aliter
C = [L]
D = [T]
The frequency (f) of a stretched string depends upon the tension F (force, length l of the string and the mass per unit length m of string. Derive the formula for frequency.
Solution
Let f = k Fa lb mc
[T–1] = k [MLT–2]a [L]b [ML–1]c
[T–1] = k [Ma+c La+b–c T–2a]
Comparing the powers a + c = 0, a + b – c = 0, – 2a = – 1
Solving these equations we get b = –1 and
or , where k is a dimensionless constant.
Write the dimensions of a and b in the relation
Where P is power, x is distance and t is time
Solution
[x] = [L] Þ [x2] = [L2]
[b] = [L2] [From principle of homogeneity]
[P] = [ML2T–3]
[a] = [M–1 T2]
Find the dimensions of where L is inductance and R is the resistance.
Solution
We know that [L] = [ML2T–2A–2] and [R] = [ML2T–3A–2]
Dimensions of is same as that of time.
Express 1 parsec in terms of meter. Write its order of magnitude.
Solution
1 parsec = 3.08 ´ 1016 m ; Here 0.5 < 3.08 < 5 \ order of magnitude = 16
Write the order of magnitude of the following measurements
(i) 45,710,000 m (ii) 92,850,000 (iii) 0.00000532 kg
Solution
(i) 45,710,000 m = 4.571 ´ 107 m
0.5 < 4.571 < 5 \ order of magnitude = 7
(ii) 92,820,000 = 0.92 ´ 108 m
0.5 < 0.92 < 5 \ order of magnitude = 8
(iii) 0.00000532 kg = 0.532 ´ 10–5
0.5 < 0.532 < 5 \ order of magnitude = – 5
Significant Figures
Significant figures in the measured value of a physical quantity tell the number of digits in which we have confidence. Larger the number of significant figures obtained in a measurement, greater is the accuracy of the measurement.
“All accurately known digits in a measurement plus the first uncertain digit together form significant figures”.
For example, when we measure the length of a straight line using a meter scale and it lies between 8.6 cm and 8.7 cm, we may estimate it as 8.64 cm. This expression has three significant figures, out of these 8 and 6 are precisely known but last digit 4 is only approximately known.
Rules for counting significant figures
For counting significant figures, we use the following rules:
Rule 1 : All non-zero digits are significant. For example x = 2567 has four significant figures.
Rule 2 : The zeroes appearing between two non-zero digits are counted in significant figures. For example 6.028 has 4 significant figures.
Rule 3 : The zeroes occurring to the left of last non-zero digit are NOT significant. For example 0.0042 has 2 significant figures.
Rule 4 : In a number without decimal, zeroes to the right of non-zero digit are NOT significant. However when some value is recorded on the basis of actual measurement the zeroes to the right of non-zero digit become significant. For example L= 20 m has two significant figures but x = 200 has only one significant figure.
Rule 5 : In a number with decimal, zeroes to the right of last non-zero digit are significant. For example
x = 14.00 has four significant digits.
Rule 6 : The powers of ten are NOT counted as significant digit. For example 1.4 ´ 107 has only two
significant digits 1 and 4.
Rule 7 : Change in the units of measurement of a quantity does not change the number of significant figures. For example, suppose distance between two stations is 4067 m. It has four significant figures. The same distance can be expressed as 4.067 km or 4.067 ´ 105 cm. In all these expressions, number of significant digits is four.
See the following table
Measured value |
Number of significant digits |
Rule number |
| 12376 | 5 | 1 |
| 6024.7 | 5 | 2 |
| 0.071 | 2 | 3 |
| 410 m | 3 | 4 |
| 720 | 2 | 4 |
| 2.40 | 3 | 5 |
| 1.6 ´ 10–17 | 2 | 6 |
Rounding off a digit
Certain rules are applied in order to round off the measurement.
Rule 1 : If the number lying to the right of digit to be rounded off is less than 5, then the rounded digit is retained as such. However if it is more than 5, then the digit to be rounded is increased by 1.
For example, x = 6.24 is rounded off to 6.2 to two significant digits and x = 8.356 is rounded off to 8.36 to three significant digits.
Rule 2 : If the digit to be dropped is 5 followed by digits other than zero then the preceding digit is increased by 1.
For example, x = 14.252 is rounded off to x = 14.3 to three significant digits.
Rule 3 : If the digit to be dropped is simply 5 or 5 followed by zero, then the preceding digit is left unchanged if it is even.
For example, x = 6.250 or x = 6.25 becomes x = 6.2 after rounding off to two significant digits.
Rule 4 : If the digit to be dropped is 5 or 5 followed by zero, then the preceding digit is raised by one if it is odd.
For example, x = 6.350 or x = 6.35 becomes x = 6.4 after rounding off to two significant digits.
See the following table
Measured value |
After rounding off to three significant digits |
Rule number |
| 7.364 | 7.36 | 1 |
| 7.367 | 7.37 | 1 |
| 8.3251 | 8.33 | 2 |
| 9.445 | 9.44 | 3 |
| 9.4450 | 9.44 | 3 |
| 15.75 | 15.8 | 4 |
| 15.7500 | 15.8 | 4 |
Algebraic operations with significant figures
In addition, subtraction, multiplication or division, inaccuracy in the measurement of any one variable affects the accuracy of final result. Hence, in general, the final result has significant figures according to the rules given below.
(i) Addition and Subtraction:
The number of decimal places in the final result (of any of these two operations) has to be equal to the SMALLEST NUMBER OF DECIMAL PLACES in any of the terms involved in calculation.
Example: 1.2 + 3.45 + 6.789 = 11.439 » 11.4
Here, the least number of significant digits after the decimal is one. Hence the result will be 11.4 (when rounded off to smallest number of decimal places).
Example: 12.63 – 10.2 = 2.43 » 2.4
(ii) Multiplication and Division:
In these operations, the number of significant figures in the result is same as the SMALLEST NUMBER OF SIGNIFICANT FIGURES in any of the factors.
Example: 1.2 ´ 1.3 = 1.56 » 1.6
The least number of significant digits on the measured values is 2. Hence the result is 1.6 (when rounded off to smallest number of significant digits)
Example: 1.2 ´ 36.72 = 44.064 » 44
Example:
Errors in measurement
“Resolution” stands for least count or the minimum reading which an instrument can read.
Accuracy: An instrument is said to be accurate if the physical quantity measured by it resembles very closely to its true value.
Precision: An instrument is said to have high degree of precision, if the measured value remains unchanged, howsoever, large number of times it may have been repeated.
There are many causes of errors in measurement. Errors may be due to instrumental defects, ignoring certain facts, carelessness of experimenter, random change in temperature, pressure, humidity, etc. When an experimentar tries to reach accurate value of measurement by doing large number of experiments, the mean of a large number of the results repeated experiments is close to the true value.
Calculation of Magnitude of Errors
(i) True value:
If a1, a2, a3 ……… an are the observed values of a measurement, then true value of measurement is the mean of these observed values.
(ii) Absolute error:
The absolute errors in various individual measured values are found by subtracting the observed value from true value. Thus,
Da1 = a0 – a1, Da2 = a0 – a2, Da3 = a0 – a3 ………. Dan = a0 – an
The absolute error may be positive or negative or zero.
(iii) Mean absolute error:
The arithmetic mean of the magnitudes of different values of absolute errors is known as the mean absolute error
(iv) Relative error or fraction error:
The ratio of the mean value of absolute error to the true value is known as the ‘mean relative error’.
When expressed in terms of percentage, relative error is called “relative percentage error”. Hence
Propagation of Errors
Suppose we want to get the volume of a sphere, . This involves multiplication of radius three times. The measurement of radius has some error, then what will be error in calculating the volume of sphere? The error in final result depends on the individual measurement as well as the mathematical operations involved in calculating the result. To calculate the net error in the result, we should study the propagation of errors in the several mathematical operations.
(1) Error in addition
Let x = a + b. suppose ± Da is absolute error in a and ± Db is absolute error in b, then we have
(2) Error in subtraction
Thus, the maximum possible error in subtraction of quantities is equal to the sum of their absolute errors.
% error in x is
(3) Error in product
The maximum fractional error in x is . Thus the maximum fractional error in the product is equal to the sum of fractional errors in the individual quantities.
(4) Error in quotient (or division)
As the terms and are small, their product can be neglected. Thus maximum fractional error is given by
And maximum possible percentage error in x is
(5) Error in the power of quantity
Let x = ap
Let
or,
or
Maximum percentage error in x is
The fractional error in the quantity raised to power ‘p’ is p times the fractional error in that quantity.
(6) General case
If then the maximum possible fractional error in x is
And the maximum possible percentage error is
| Illustrations |
State the number of significant figures in the following
(i) 0.007 m2 (ii) 2.64 ´ 1024 kg (iii) 0.2370 g cm–3 (iv) 6.320 J
(v) 6.032 Nm–2 (vi) 0.0006032 m2 (vii) 2.000 m (viii) 5100 kg (ix) 0.050 cm
Solution
(i) one : 7 (ii) three : 2, 6, 4 (iii) four : 2, 3, 7, 0 (iv) four : 6, 3, 2, 0
(v) four : 6, 0, 3, 2 (vi) four : 6, 0, 3, 2 (vii) four : 2, 0, 0, 0 (viii) four : 5, 1, 0, 0
(ix) two : 5, 0
| f | 5100 kg is a measured value, and so it has four significant figures. If it is simply a numerical value, 5100, then number of significant digits would be two. |
Solve the following and express the result to an appropriate number of significant figures.
(i) Add 6.2 g, 4.33 g and 17.456 g
(ii) Subtract 63.54 kg from 187.2 kg
(iii) 75.5 ´ 125.2 ´ 0.51
(iv)
(v)
Solution
(i) 6.2 g + 4.33 g + 17.456 g = 27.986 g
The result should be rounded off to first decimal place due to 6.2 g
= 28.0 g
(ii) 187.2 kg – 63.54 kg = 123.66 kg
The result should be rounded off to first decimal place due to 187.2 kg
= 123.7 kg
(iii) 75.5 ´ 125.2 ´ 0.51 = 4820.826
The result should be rounded off to two significant digits due to 0.51
= 4800
(iv)
The result should be rounded off to three significant digits because of 2.13
= 0.115
(v)
The result should be rounded off to three significant digits because of 1.81 = 1.02 ´ 104
If L = 2.5 ´ 104 and B = 3.9 ´ 105 then B – L =
(A) 1.4 ´ 104 (B) 1.4 ´ 105 (C) 3.6 ´ 104 (D) 3.6 ´ 105
Solution
Given L = 2500 and B = 390000
Now B – L = 390000 – 25000 = 365000
= 3.65 ´ 105
= 3.6 ´ 105 (rounded to one place of decimal)
The area enclosed by a circle of diameter 1.06 m to correct number of significant figures is
[take π = 3.14]
(A) 0.88 m2 (B) 0.088 m2 (C) 0.882 m2 (D) 0.530 m2
Ans (C)
Area is A = pr2 = 3.14(0.530)2 = 0.882026 m2
= 0.882 m2 (rounded to three significant digits)
Object distance, u = (50.1 ±5) cm and image distance, v = (20.1 ± 0.2) cm then focal length is
(A) (12.4 ± 0.4) cm (B) (12.4 ± 0.1) cm
(C) (14.3 ± 0.4) cm (D) (14.3 ± 0.1) cm
Ans (C)
Focal length is given by or or f = 14.345 cm = 14.3 cm
Df = 0.0299 ´ 14.3 = 0.428 = 0.4 cm
So focal length = (14.3 ± 0.4) cm
PRACTICE QUESTIONS
BIOLOGY NOTES AND PRACTICE QUESTIONSCHAPTER WISE QUESTIONS WITH SOLUTION

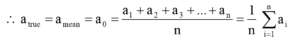


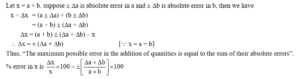



thanks